








































































































































































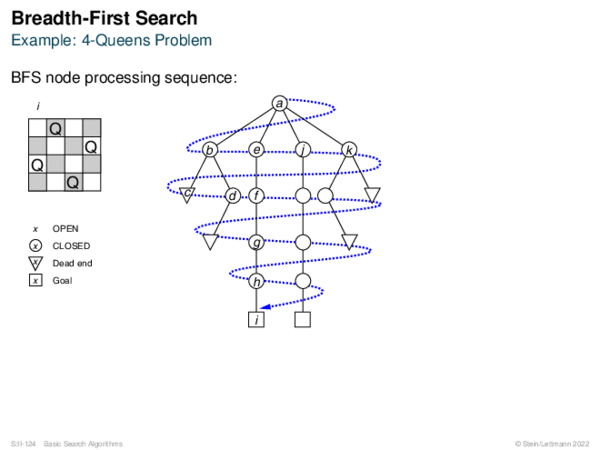
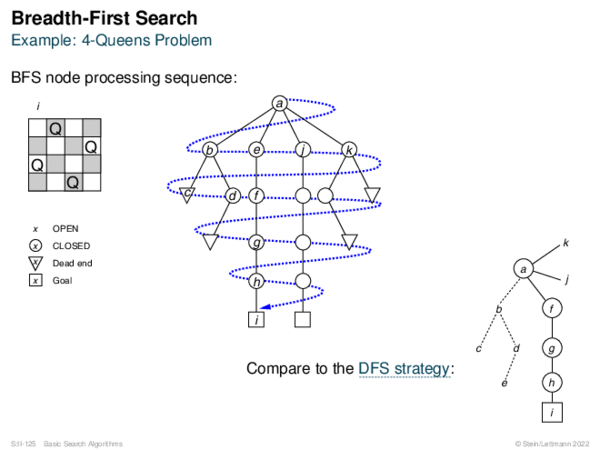

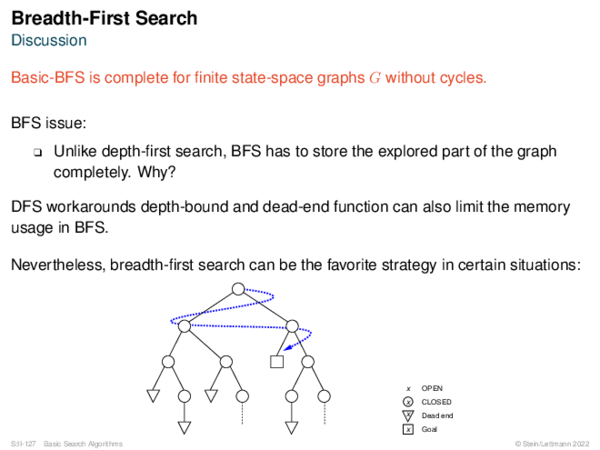



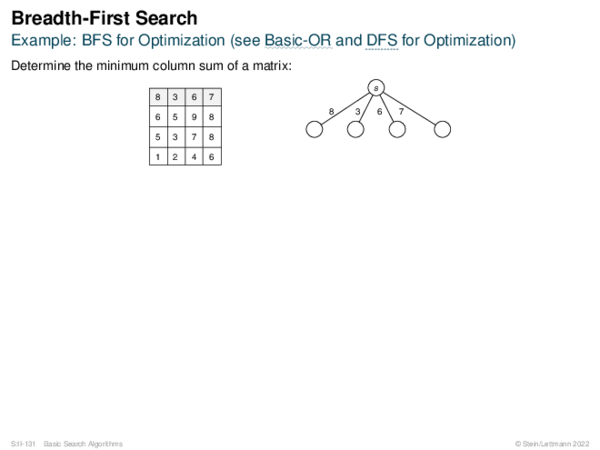























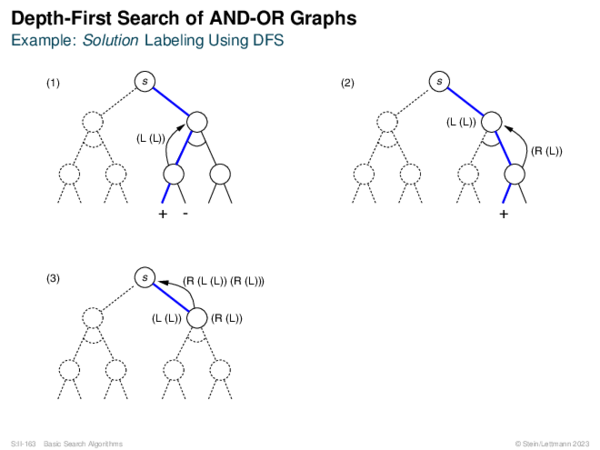



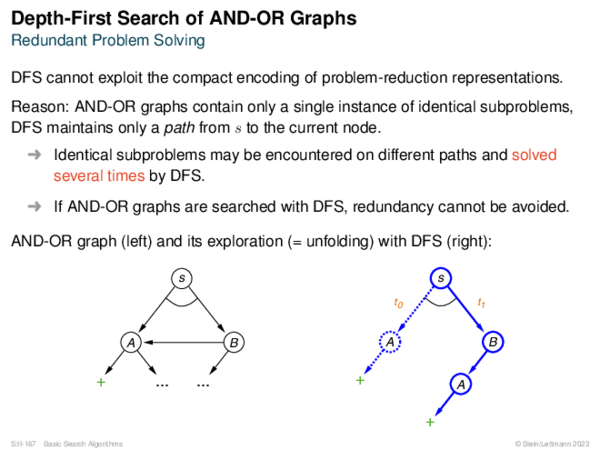

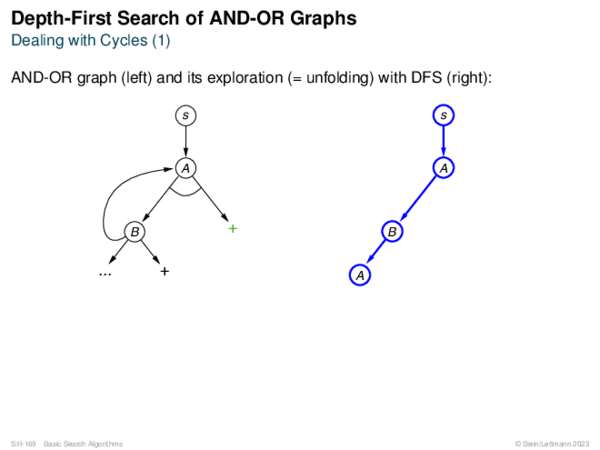
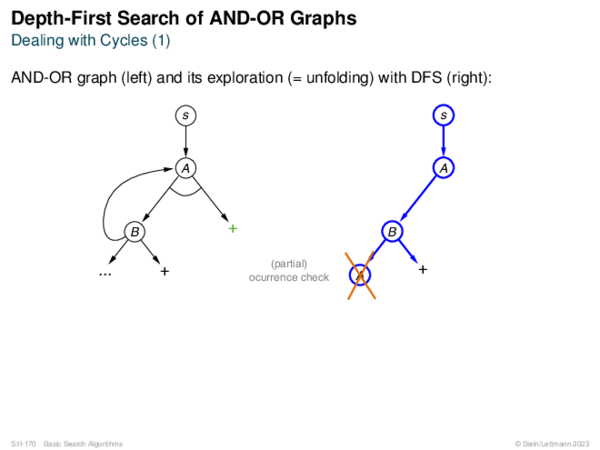
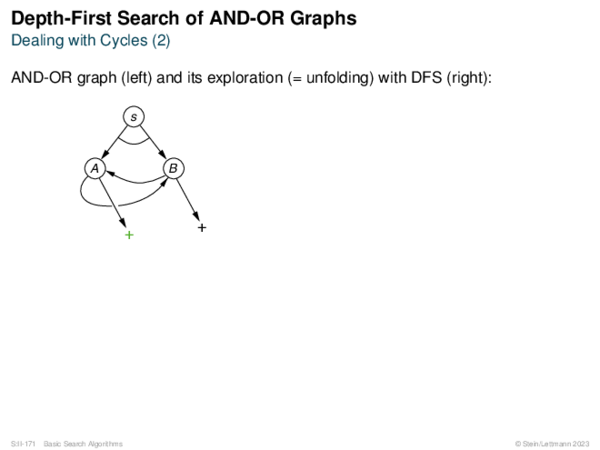
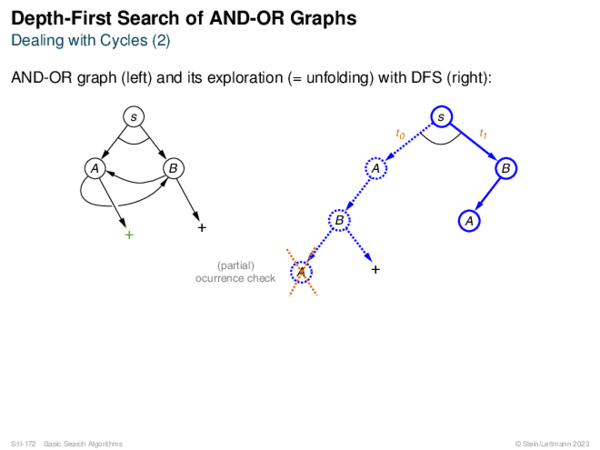
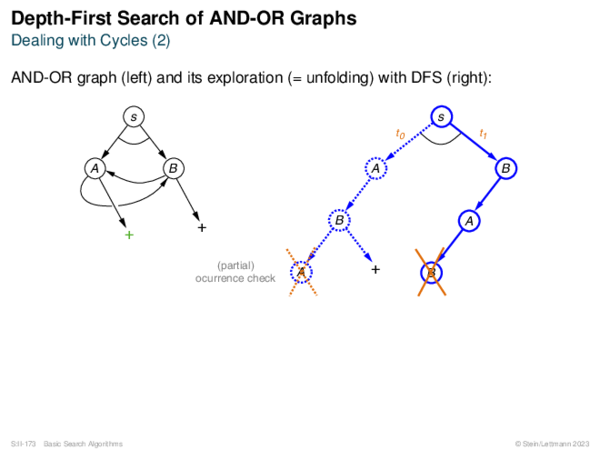
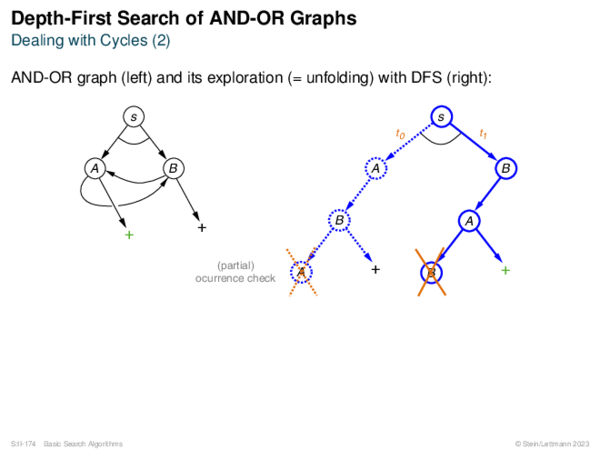







![AND-OR Graph Basics Generic_AND-OR_Tree(s, successors, ?) [Generic_OR]](https://downloads.webis.de/lecturenotes/search/unit-en-basic-search3/unit-en-basic-search3-50.png)



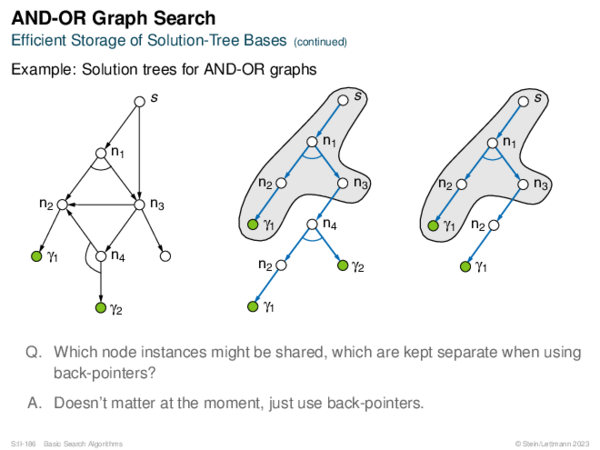



![AND-OR Graph Search Basic_AND-OR_Tree(s, successors, is_solved) [Basic_OR]](https://downloads.webis.de/lecturenotes/search/unit-en-basic-search3/unit-en-basic-search3-58.png)

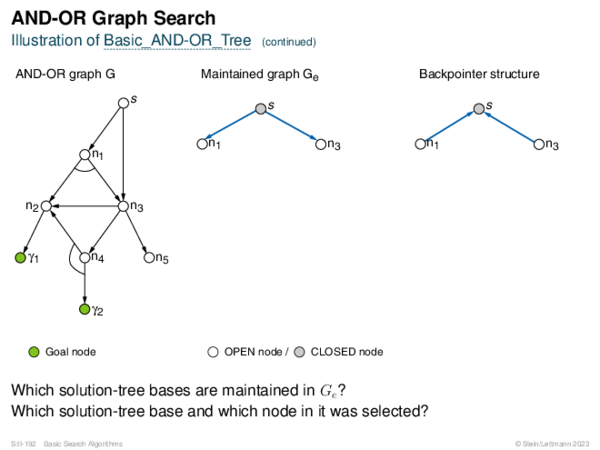
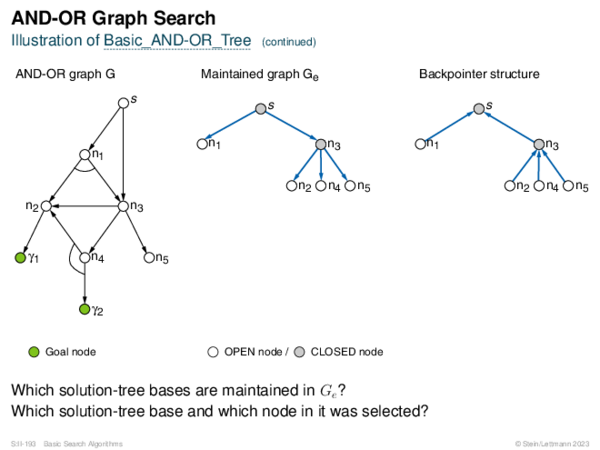
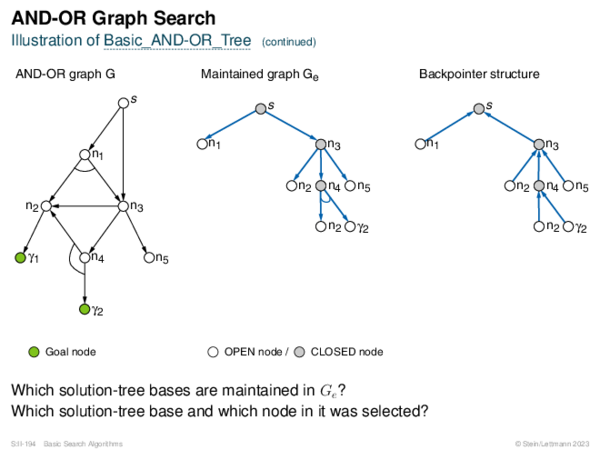
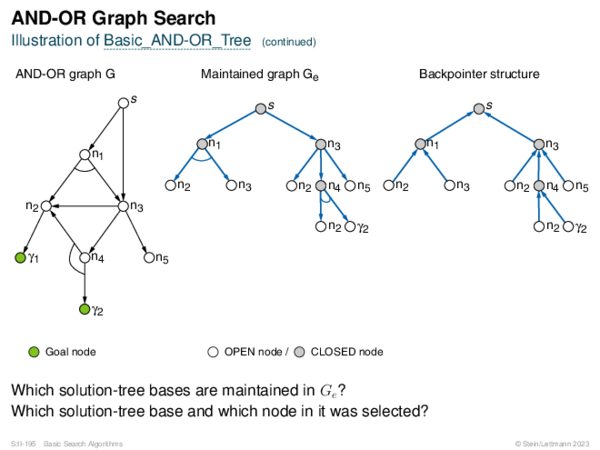
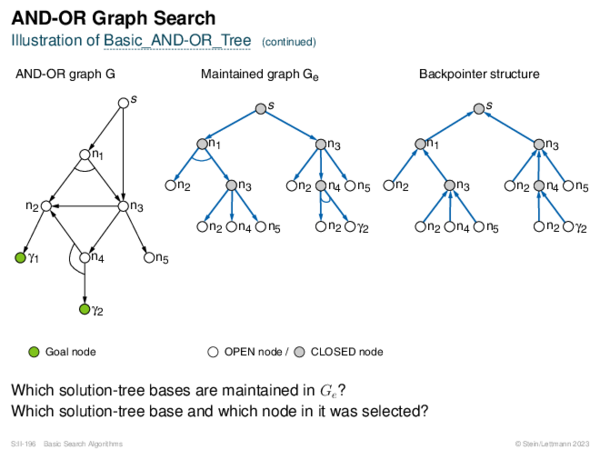
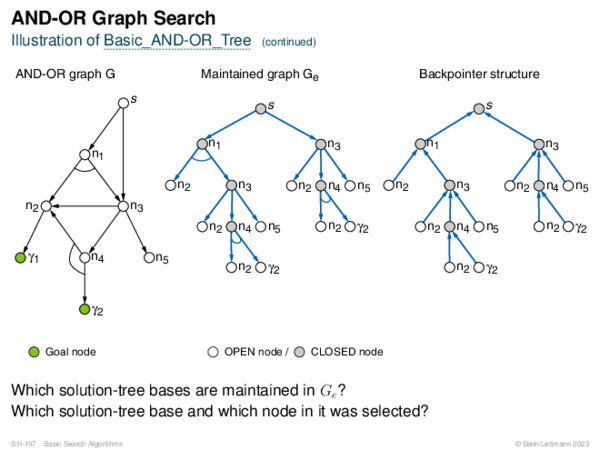
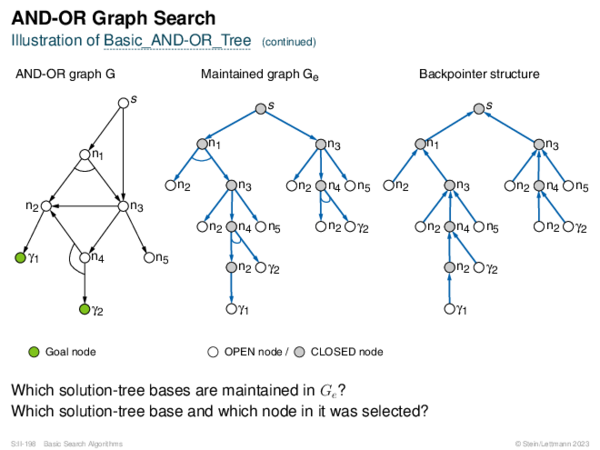



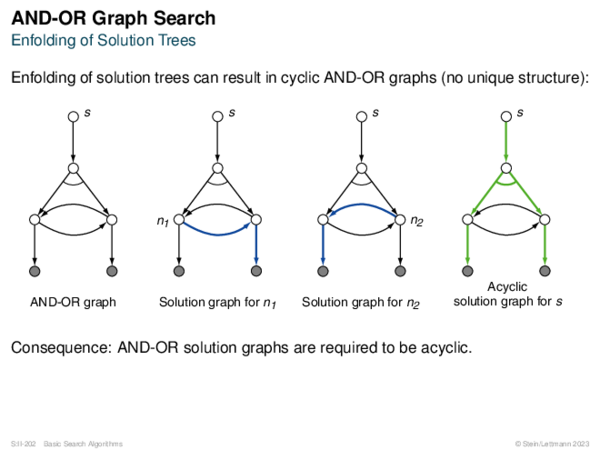
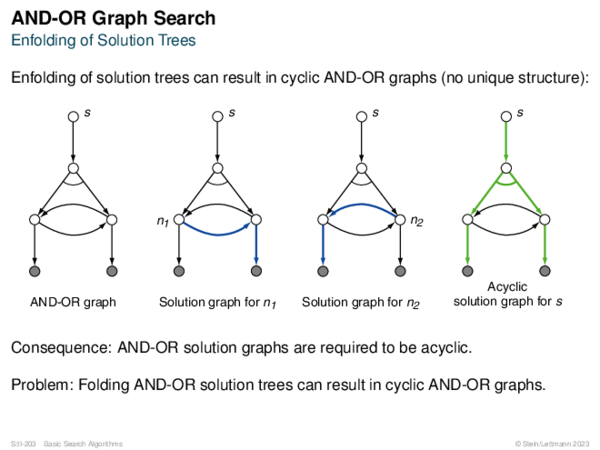
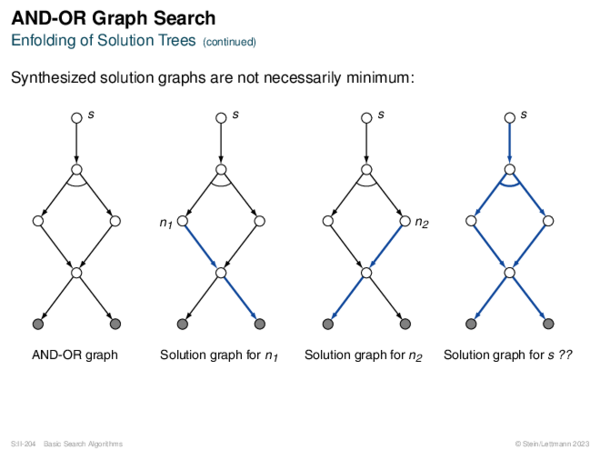
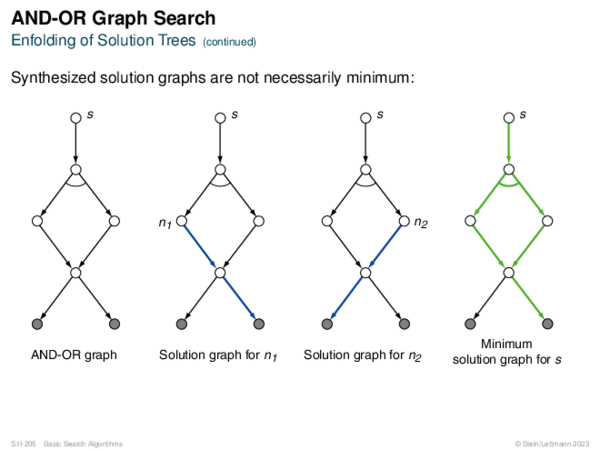
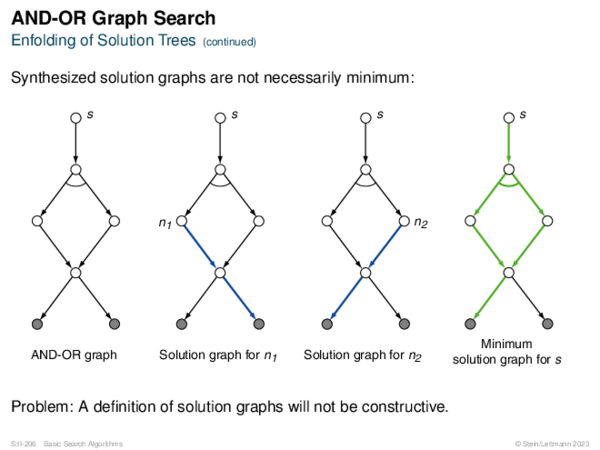







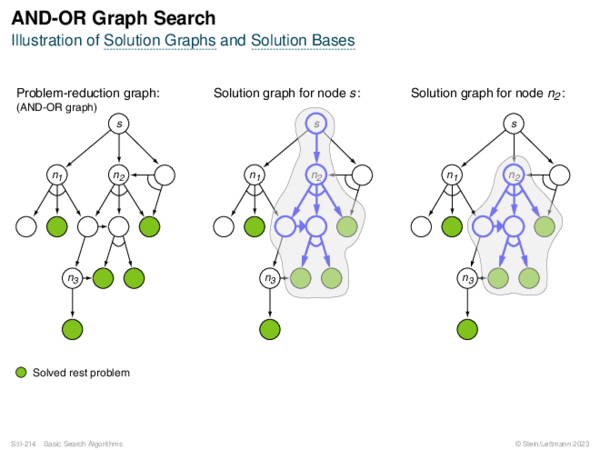

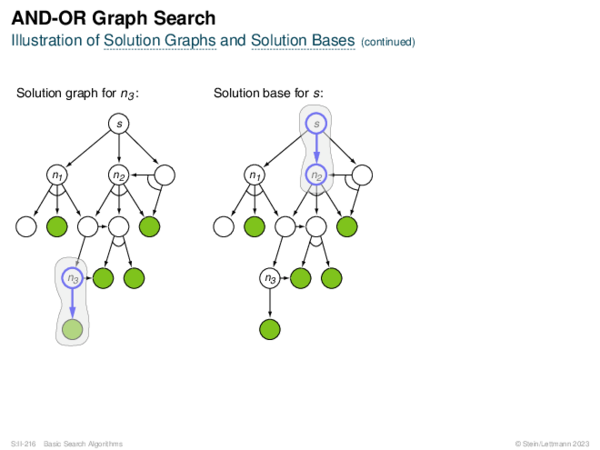



![AND-OR Graph Search Generic_AND-OR(s, successors, ?) [Generic_AND-OR_Tree] [Generic_OR]](https://downloads.webis.de/lecturenotes/search/unit-en-basic-search3/unit-en-basic-search3-88.png)

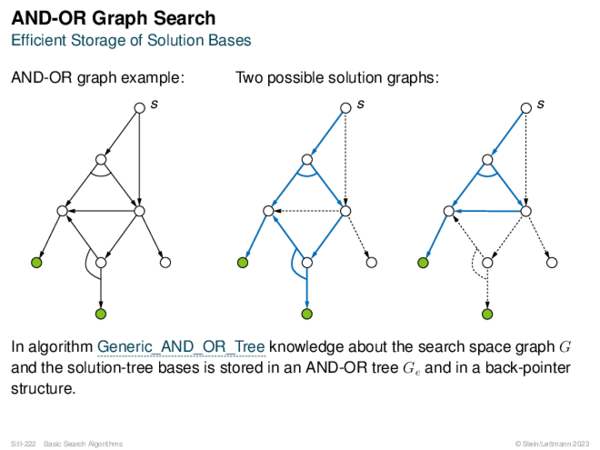




![AND-OR Graph Search Basic_AND-OR(s, successors, is_solved) [Basic_OR]](https://downloads.webis.de/lecturenotes/search/unit-en-basic-search3/unit-en-basic-search3-98.png)




















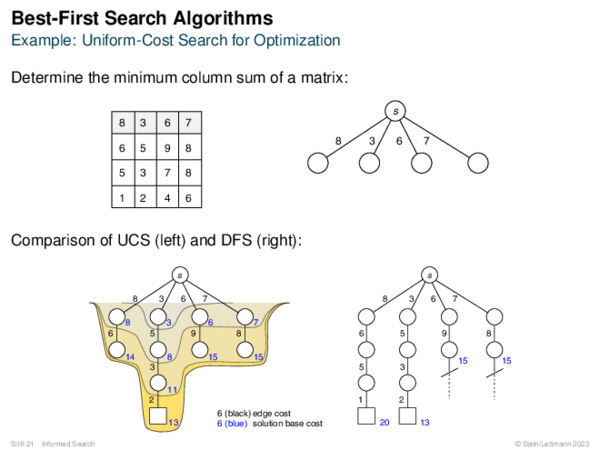










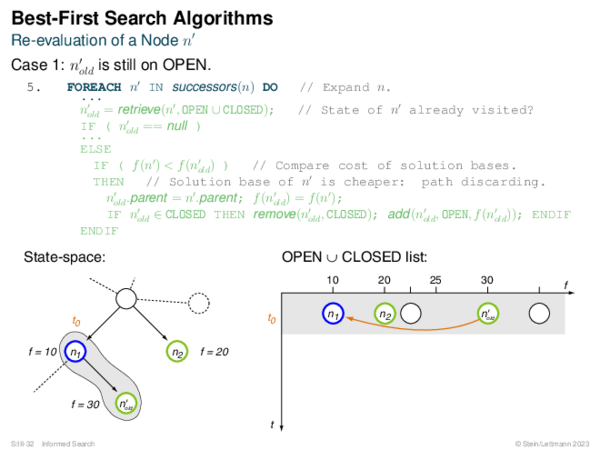
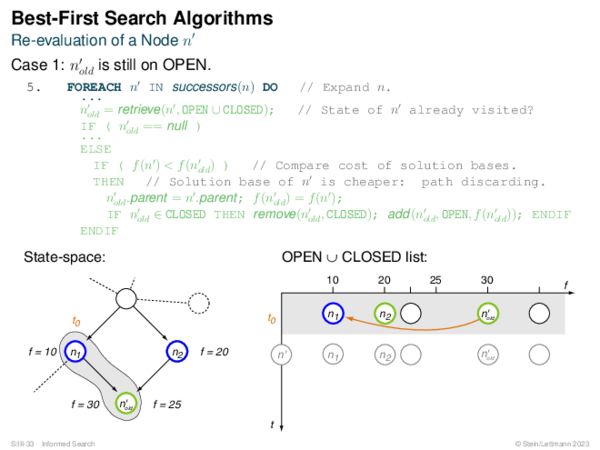
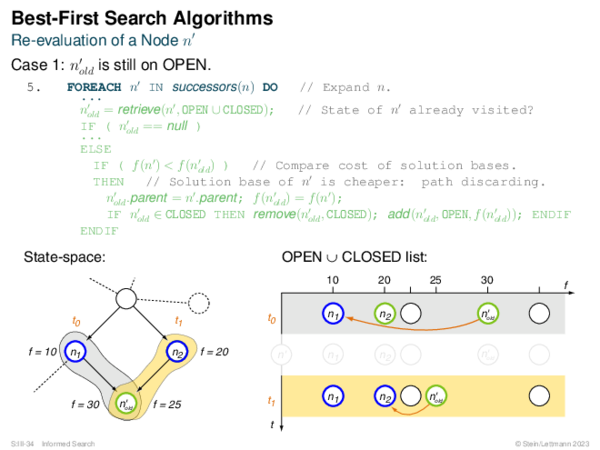

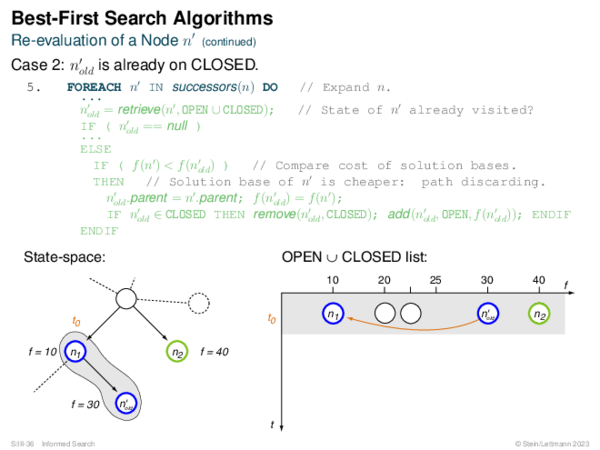
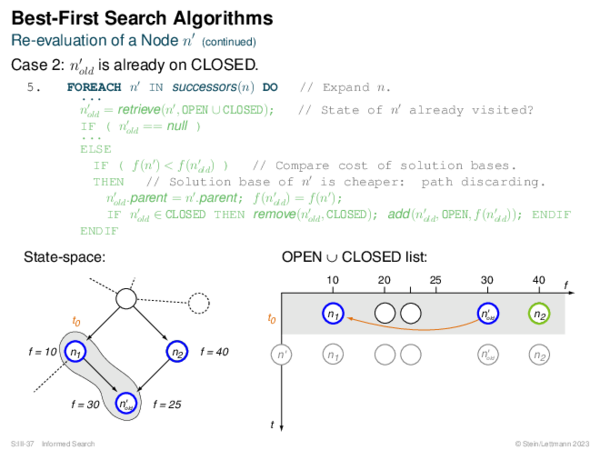
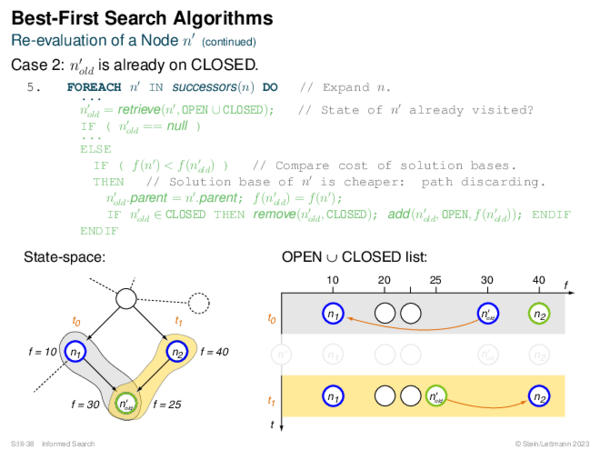





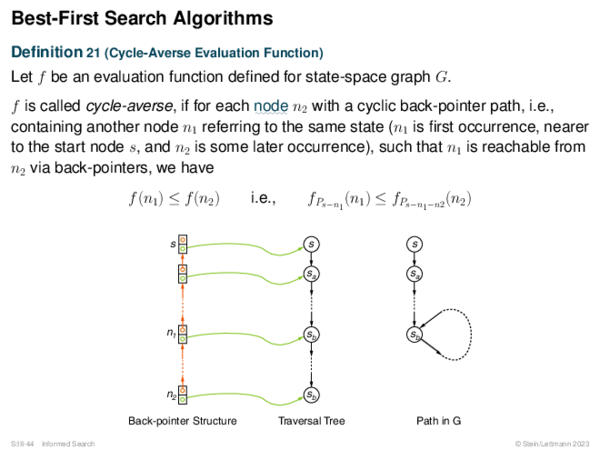








































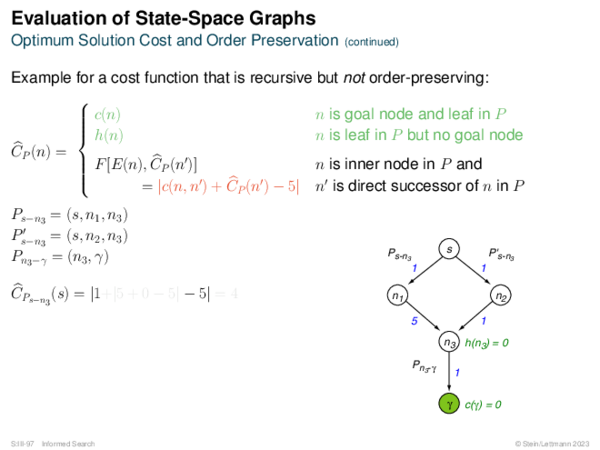
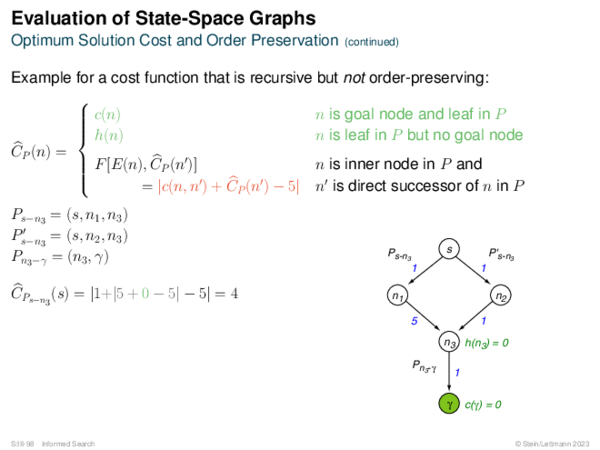
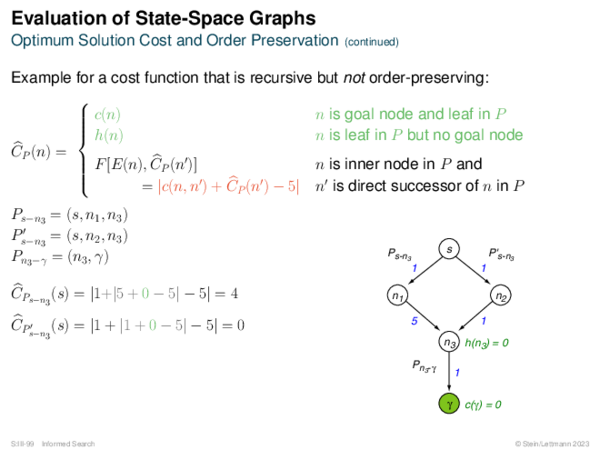
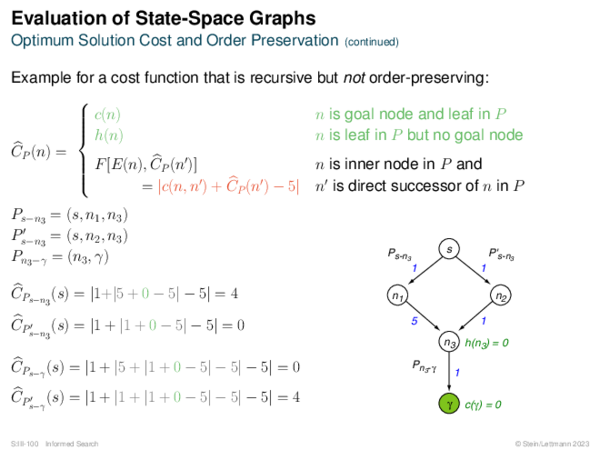

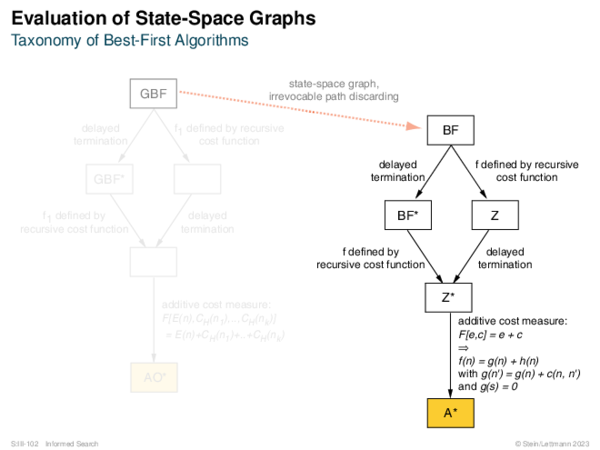







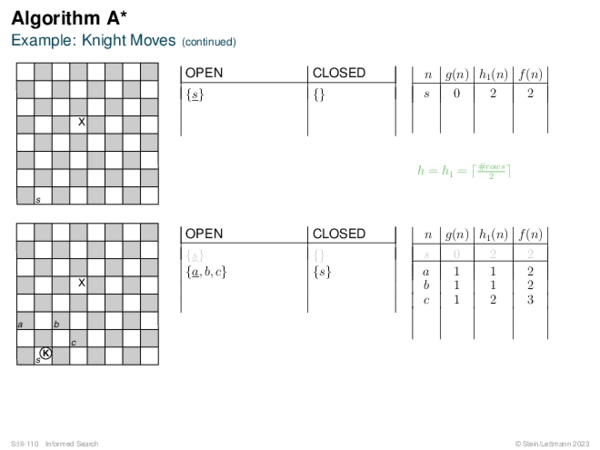


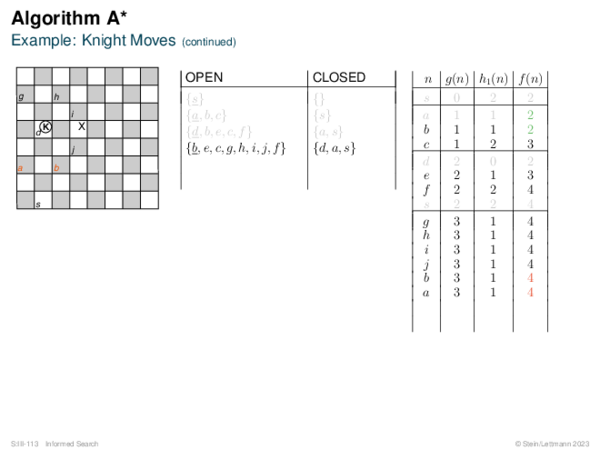
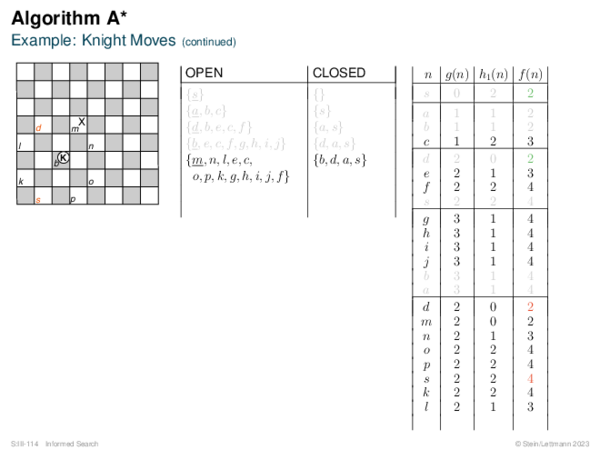
















![BF* Variants OPEN List Size Restriction: Best-First Beam Search [Rich & Knight 1991]](https://downloads.webis.de/lecturenotes/search/unit-en-informed-bf3/unit-en-informed-bf3-18.png)







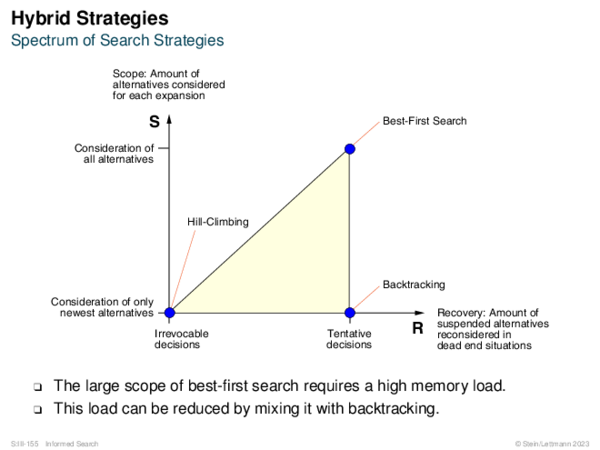

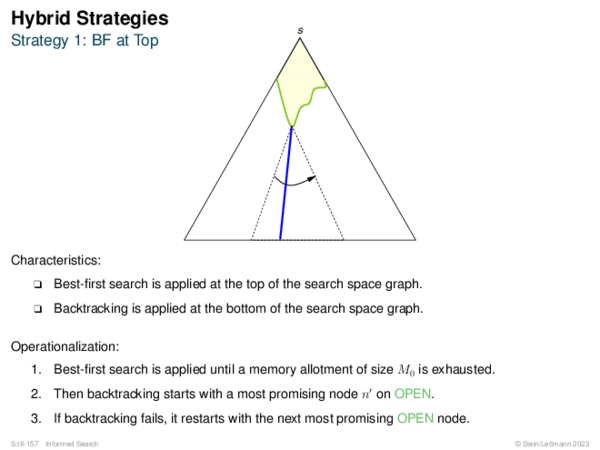
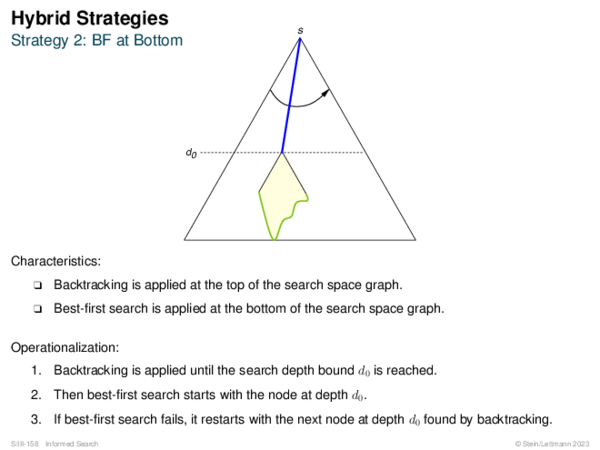




![Hybrid Strategies Strategy 4: Focal Search [Ibaraki 1978]](https://downloads.webis.de/lecturenotes/search/unit-en-informed-bf3/unit-en-informed-bf3-35.png)

![Hybrid Strategies Strategy 5: Staged Search [Nilson 1971]](https://downloads.webis.de/lecturenotes/search/unit-en-informed-bf3/unit-en-informed-bf3-37.png)

![Hybrid Strategies Strategy 6: Iterative Deepening A* – IDA* [Korf 1985]](https://downloads.webis.de/lecturenotes/search/unit-en-informed-bf3/unit-en-informed-bf3-39.png)

















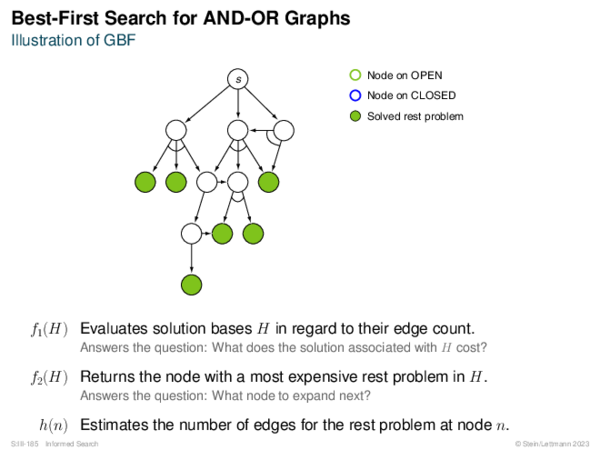



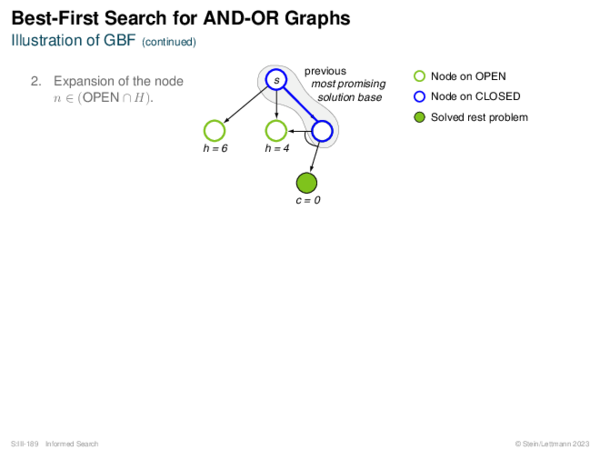
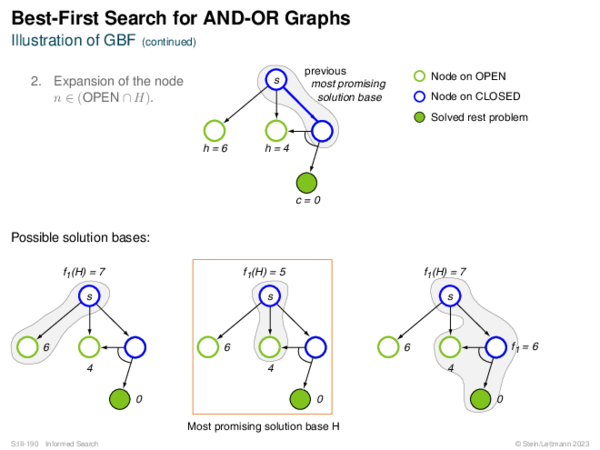
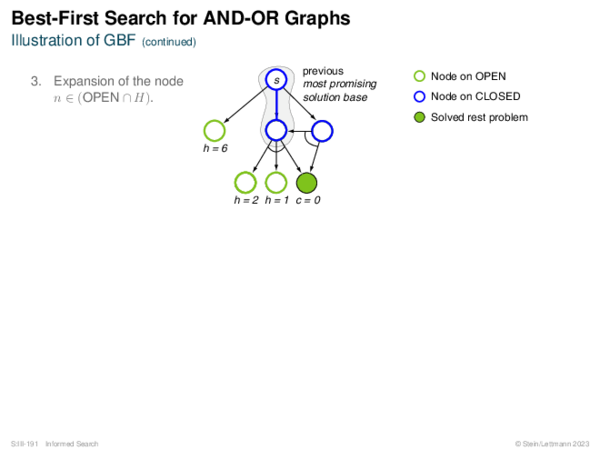

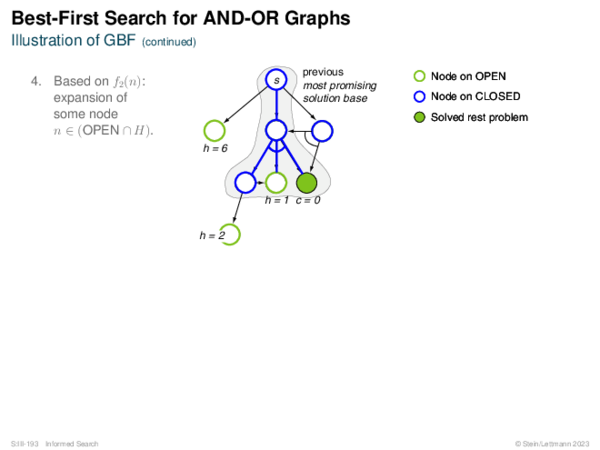
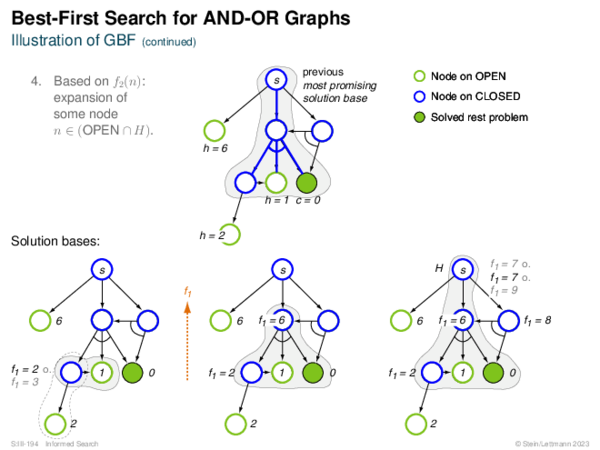
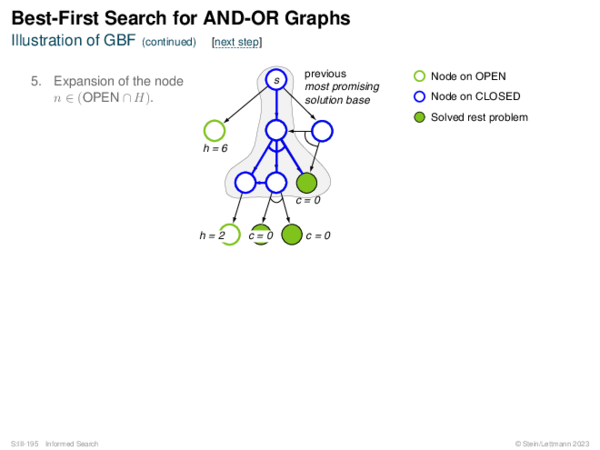
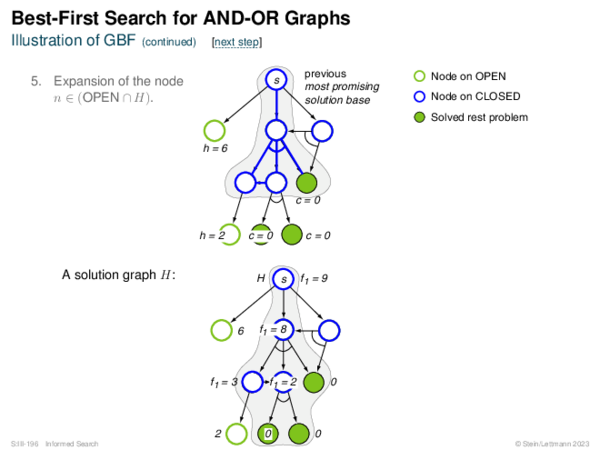
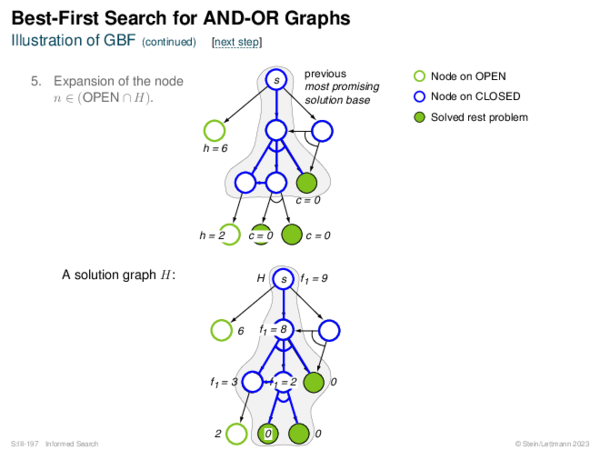
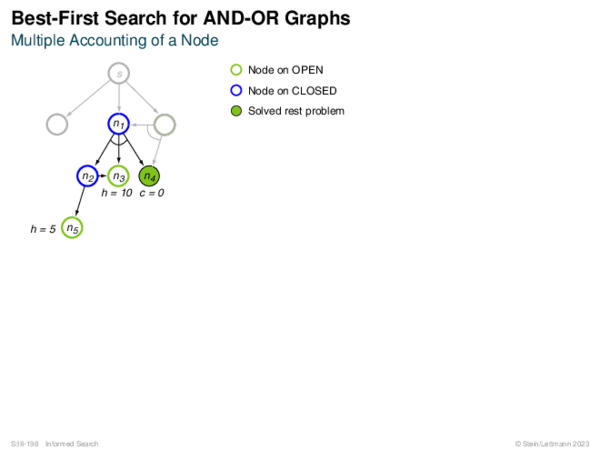
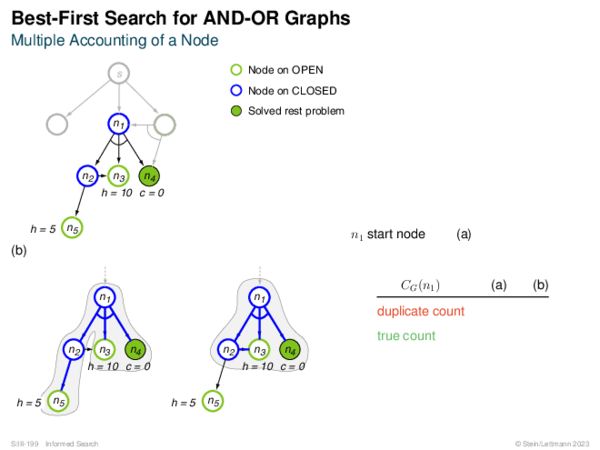
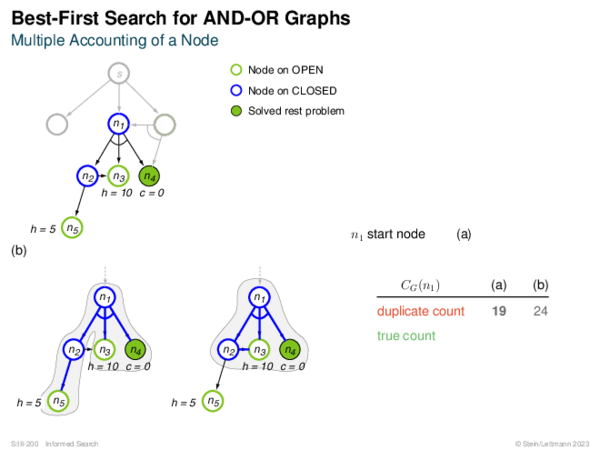
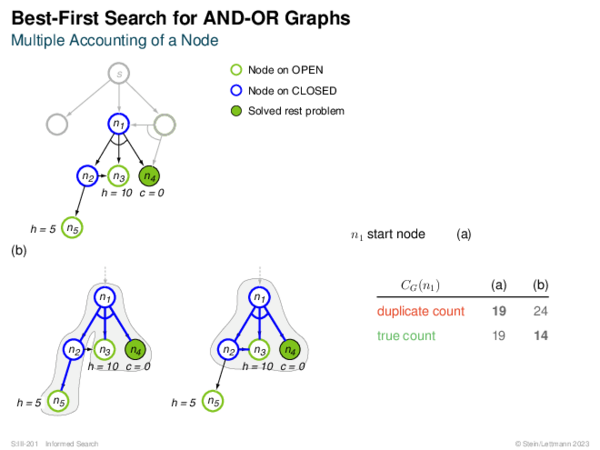




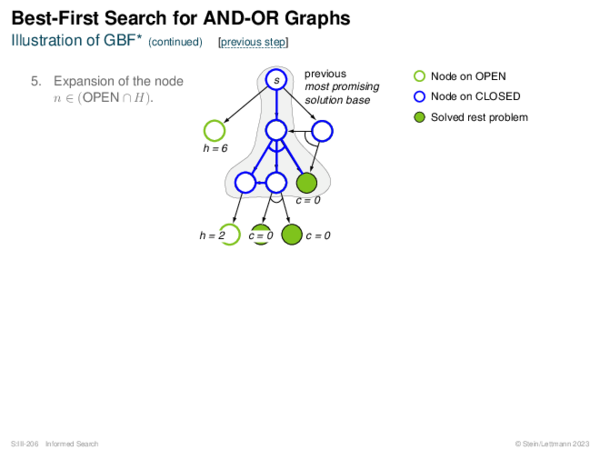
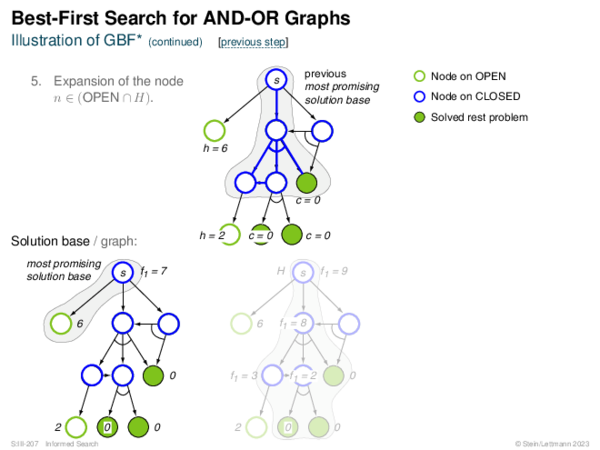

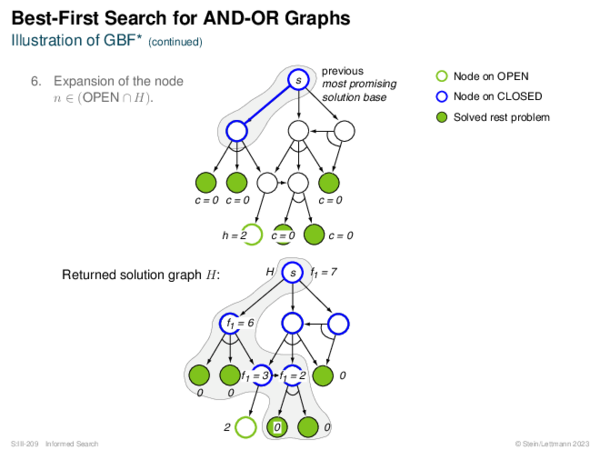
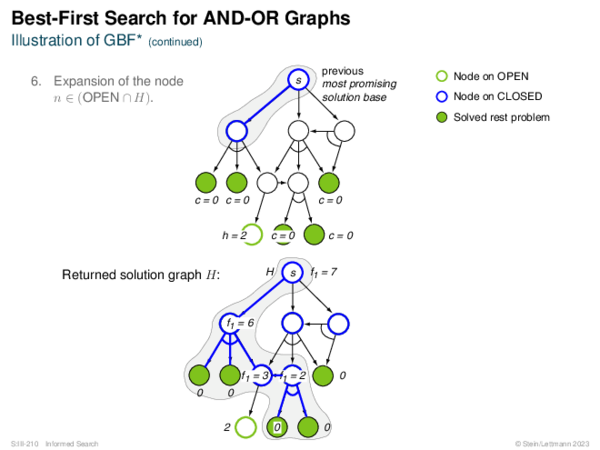







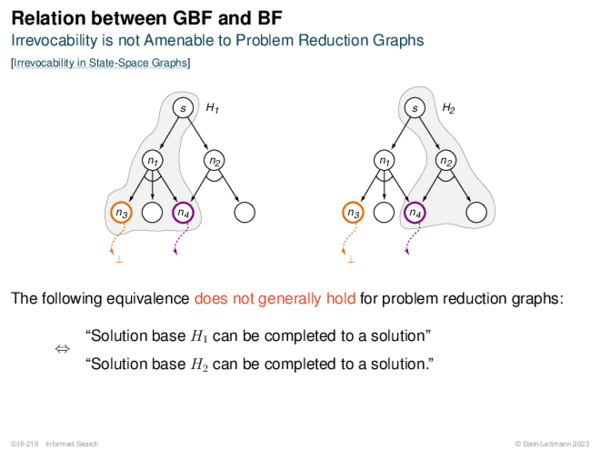




















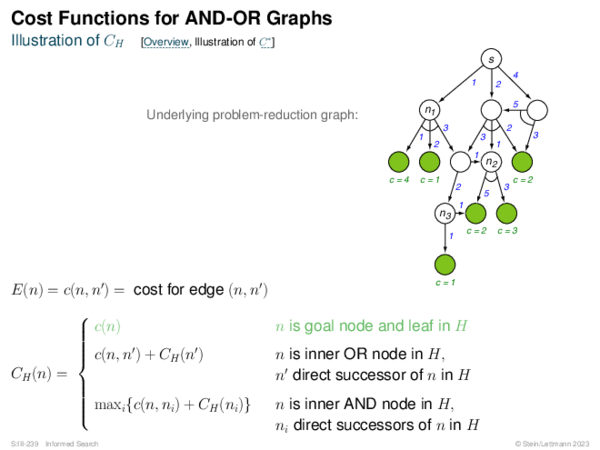
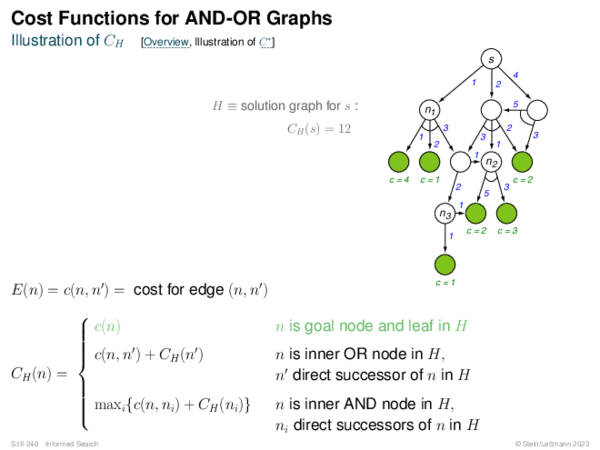
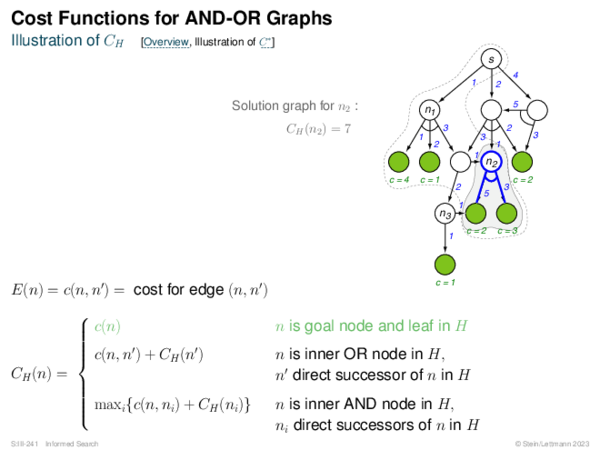
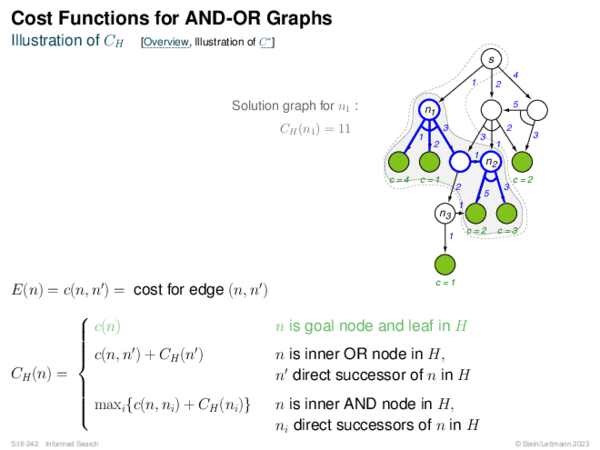
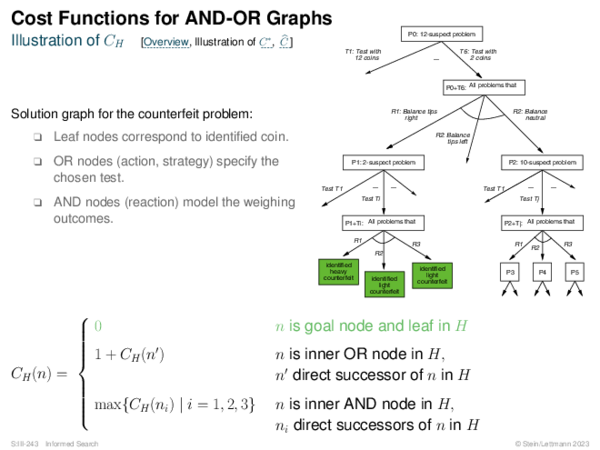
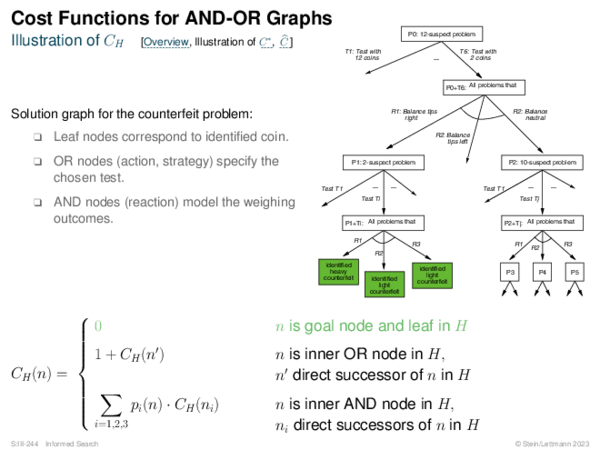





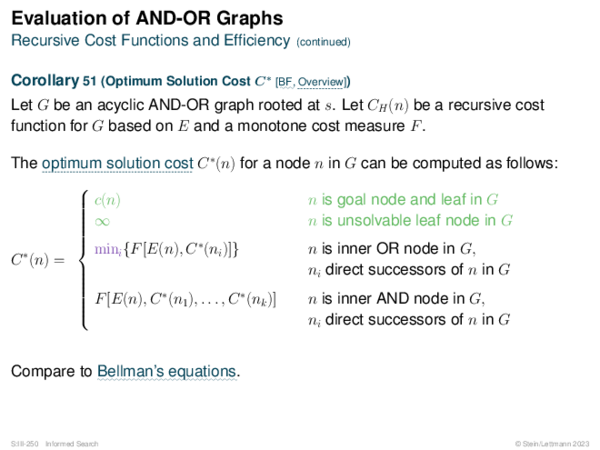
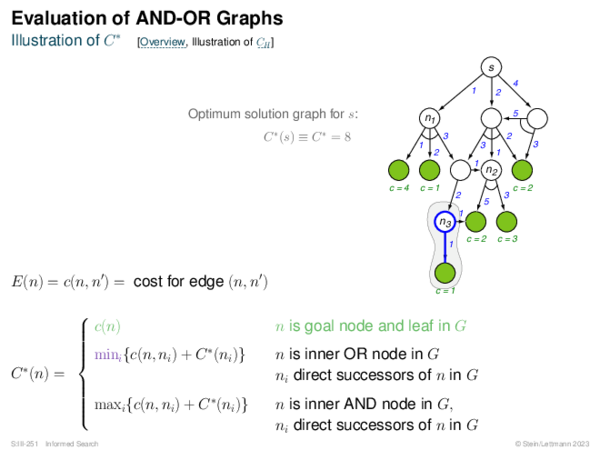
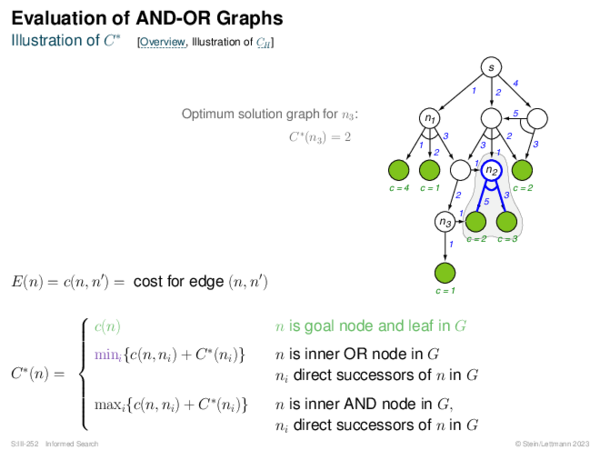
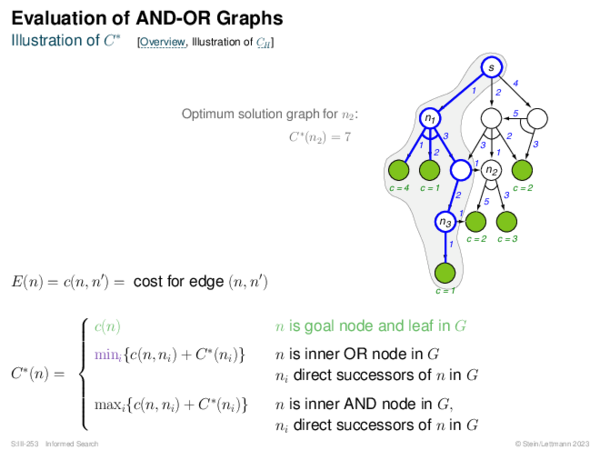
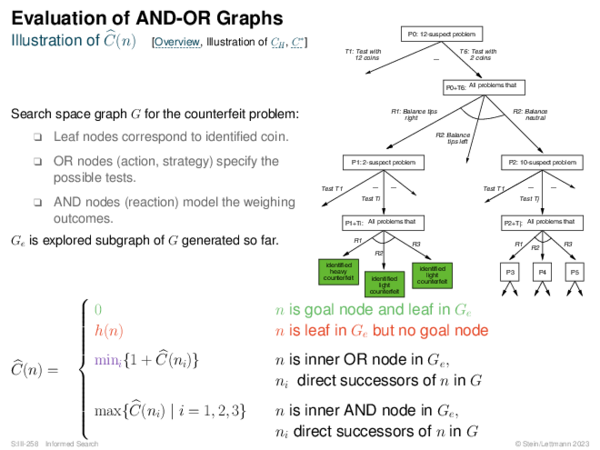
![Evaluation of AND-OR Graphs ] Illustration of C ∗](https://downloads.webis.de/lecturenotes/search/unit-en-informed-bf5/unit-en-informed-bf5-35.png)
























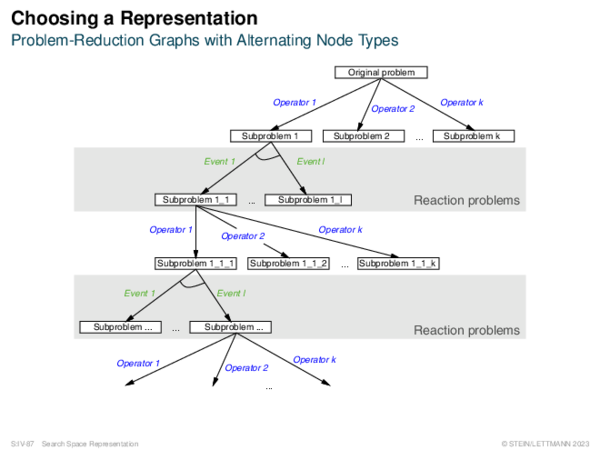
![Systematic Search Categorization of Heuristic [Problem Solving] Methods](https://downloads.webis.de/lecturenotes/search/unit-en-representation1/unit-en-representation1-19.png)
![Systematic Search Categorization of Heuristic [Problem Solving] Methods](https://downloads.webis.de/lecturenotes/search/unit-en-representation1/unit-en-representation1-20.png)





























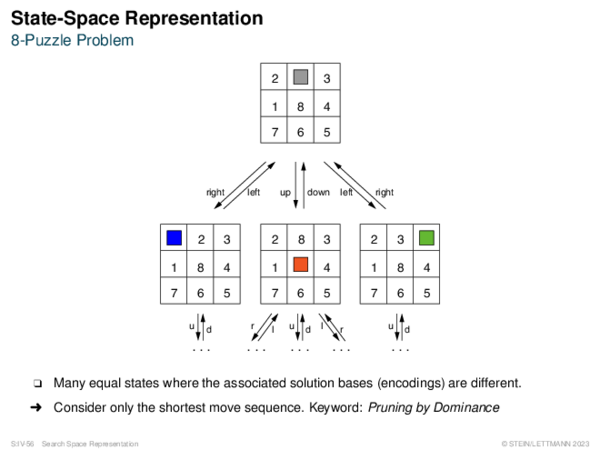












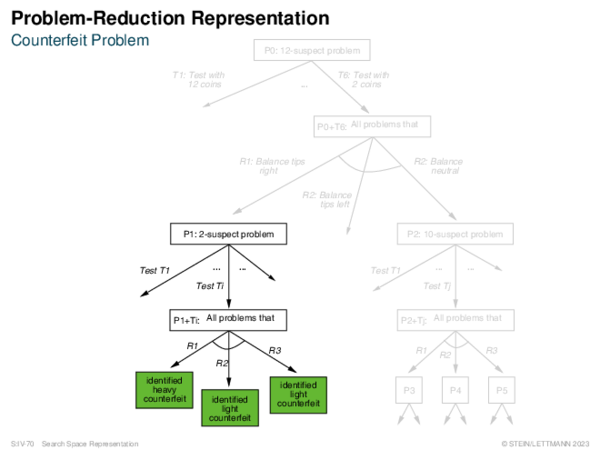



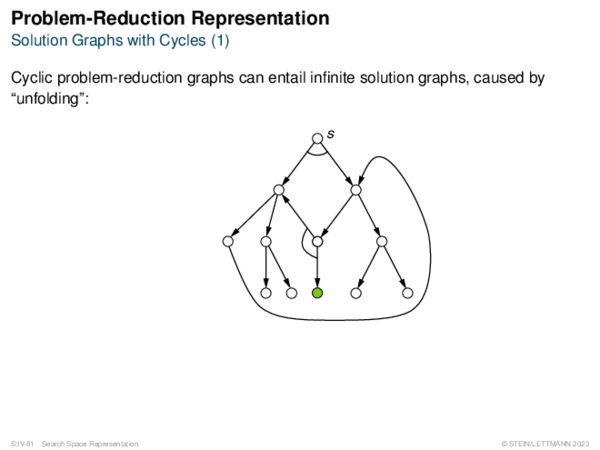
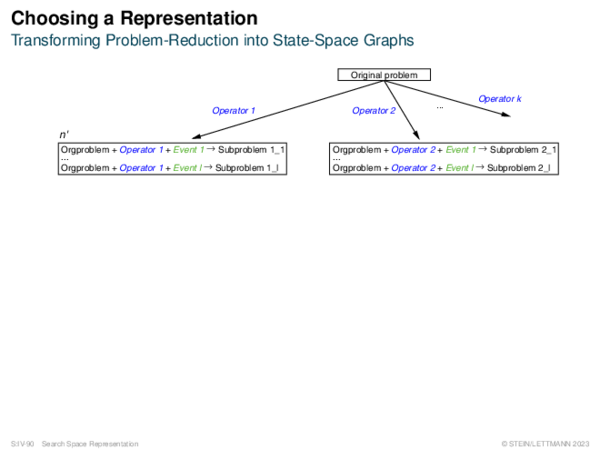
![Problem-Reduction Representation Search Building Blocks [State-Space]](https://downloads.webis.de/lecturenotes/search/unit-en-representation2/unit-en-representation2-13.png)






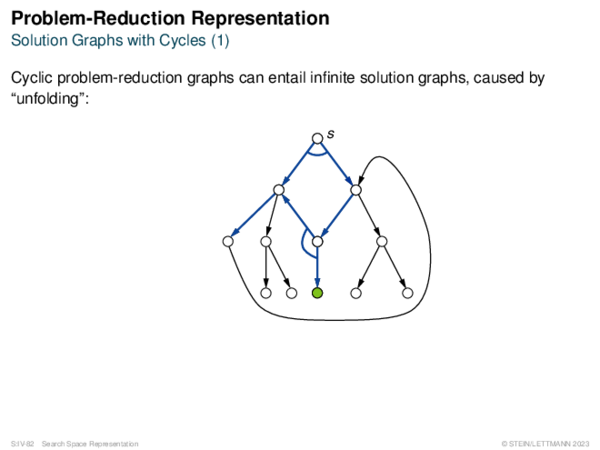
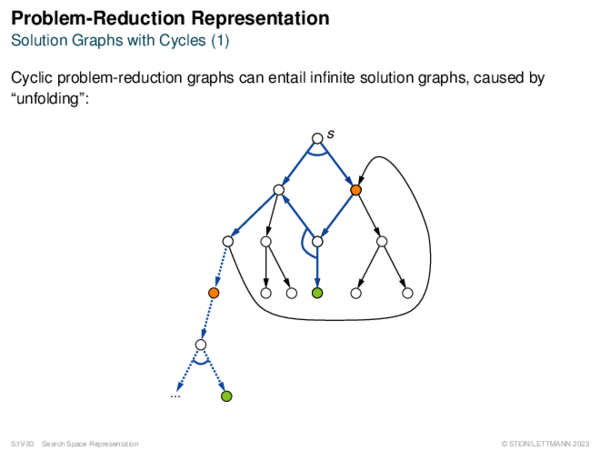

















































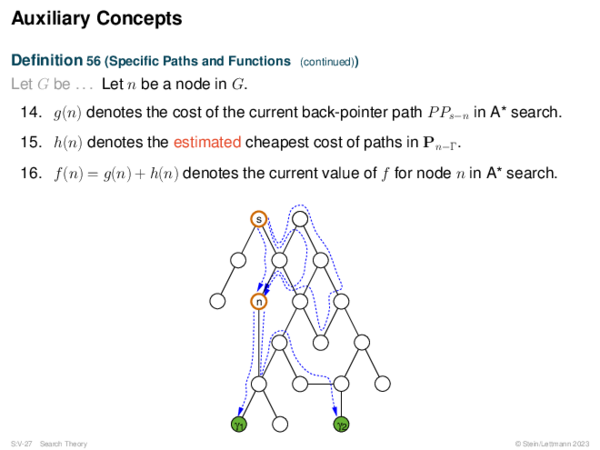











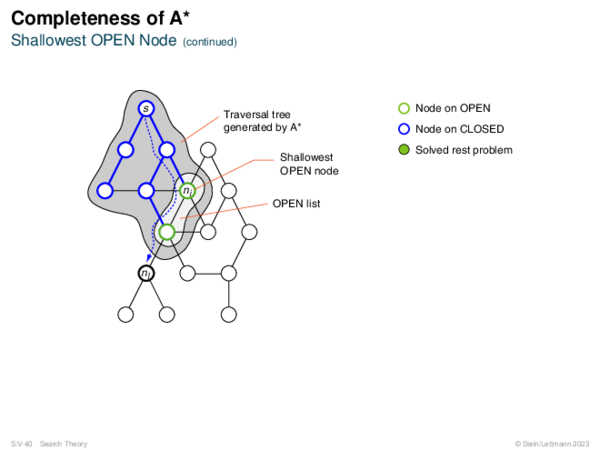
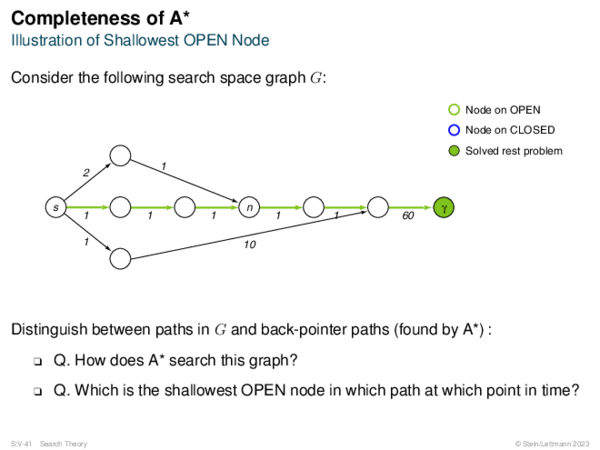
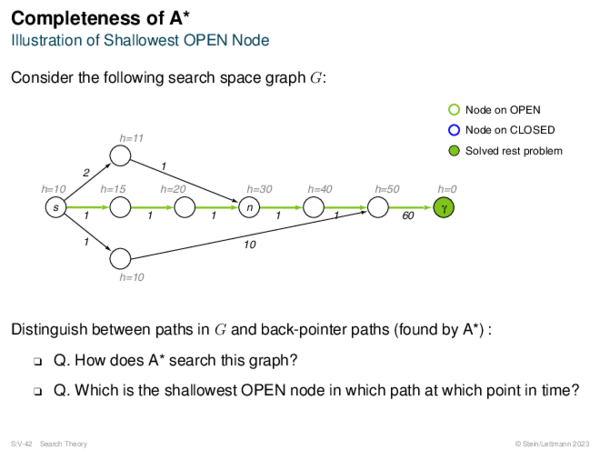
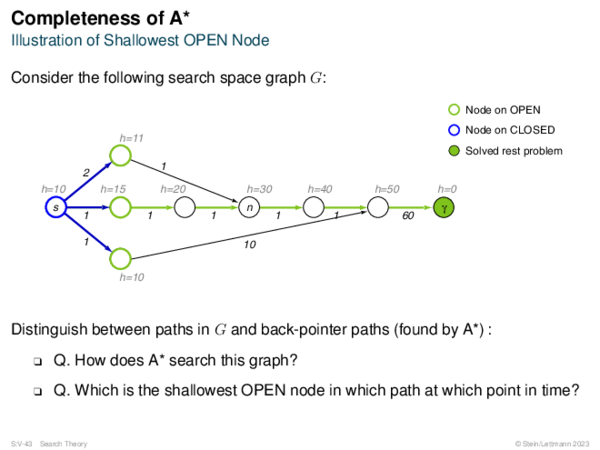
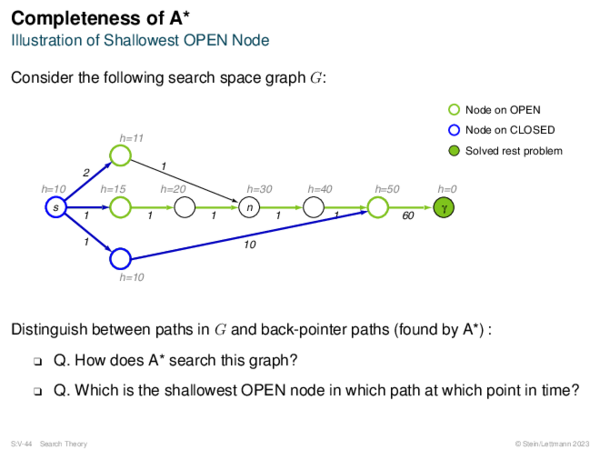
















![Admissibility of A* Corollary 67 (Shallowest OPEN Node on Optimum Path [Lemma 62])?](https://downloads.webis.de/lecturenotes/search/unit-en-astar-formal1/unit-en-astar-formal1-62.png)
![Admissibility of A* Corollary 67 (Shallowest OPEN Node on Optimum Path [Lemma 62])?](https://downloads.webis.de/lecturenotes/search/unit-en-astar-formal1/unit-en-astar-formal1-63.png)




![Admissibility of A* Theorem 69 (Admissibility [Hart, Nilsson, Raphael 1968,1972])](https://downloads.webis.de/lecturenotes/search/unit-en-astar-formal1/unit-en-astar-formal1-68.png)
![Admissibility of A* Theorem 69 (Admissibility [Hart, Nilsson, Raphael 1968,1972])](https://downloads.webis.de/lecturenotes/search/unit-en-astar-formal1/unit-en-astar-formal1-69.png)










































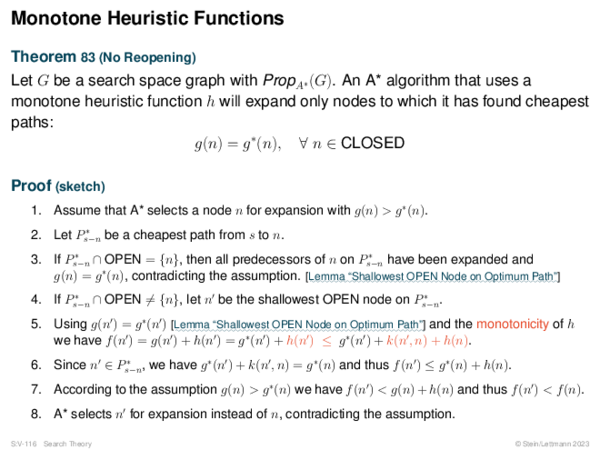

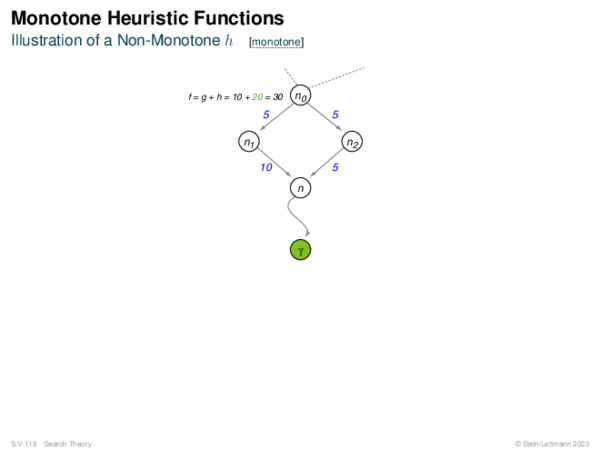
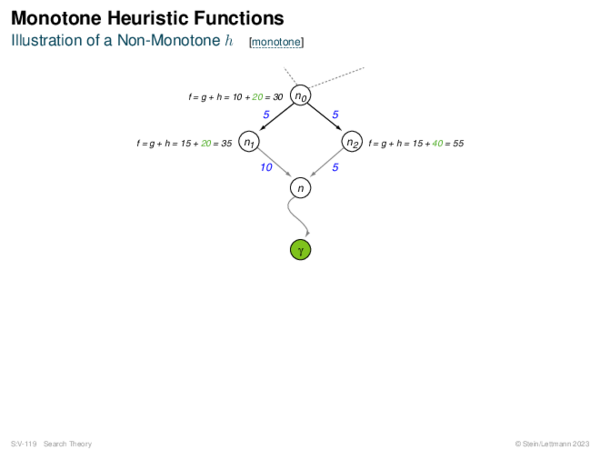
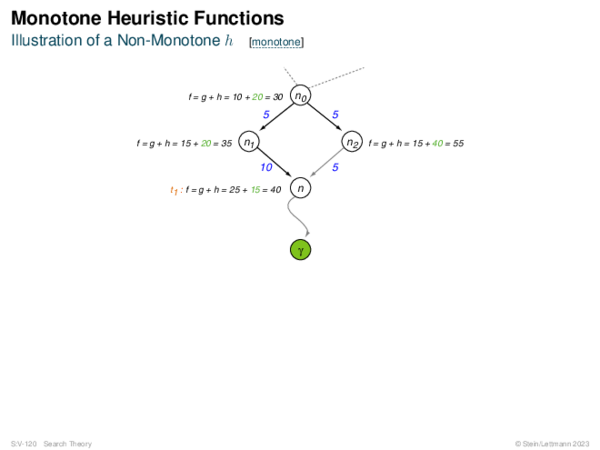






























































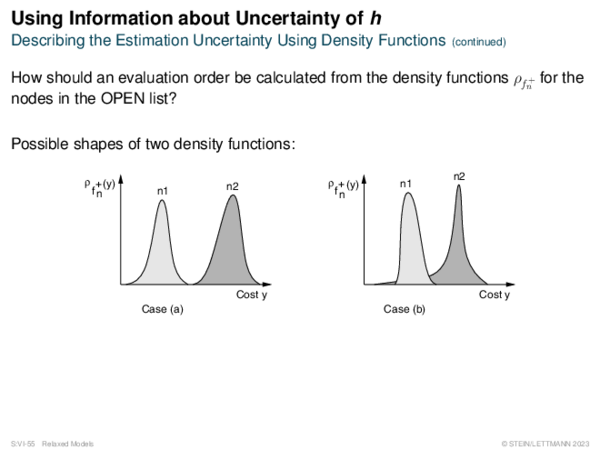





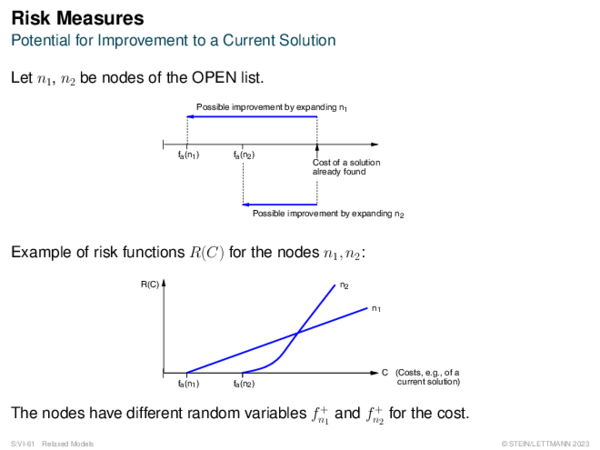

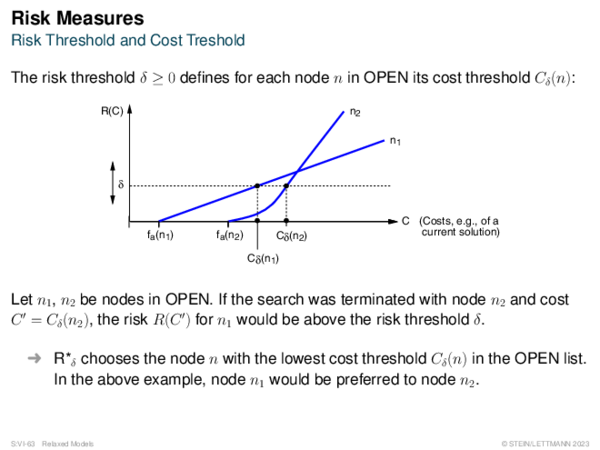




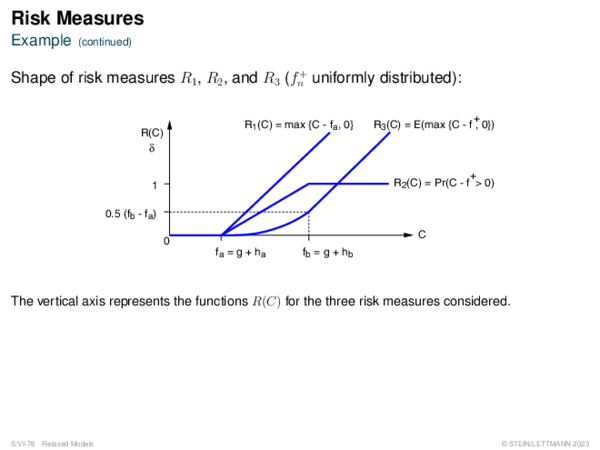
![Risk Measures Risk Measures of Type R(C) = %[C − f +]](https://downloads.webis.de/lecturenotes/search/unit-en-astar-relaxed2/unit-en-astar-relaxed2-24.png)
![Risk Measures Risk Measures of Type R(C) = %[C − f +]](https://downloads.webis.de/lecturenotes/search/unit-en-astar-relaxed2/unit-en-astar-relaxed2-25.png)











































































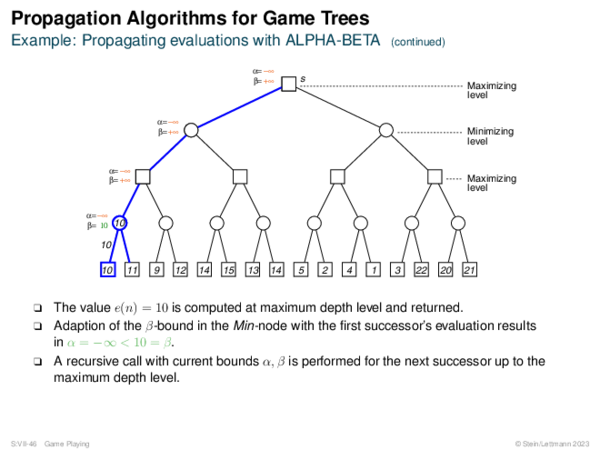

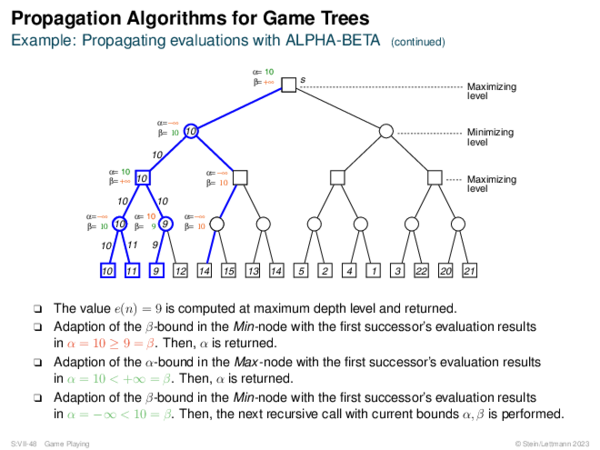
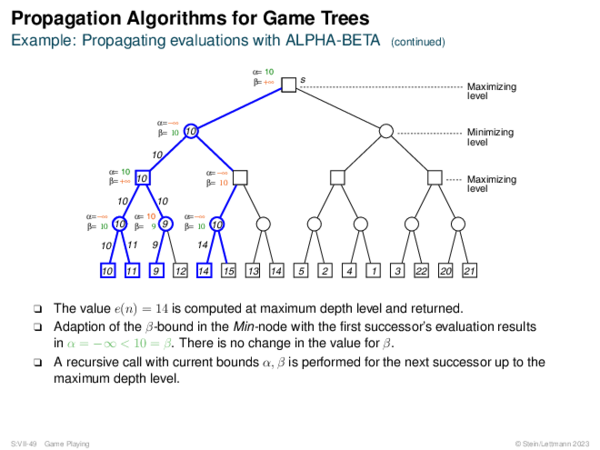
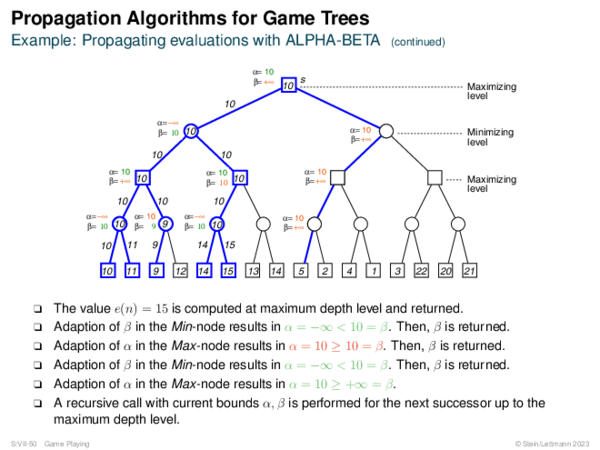
















































































































































































































































































![AND-OR Graph Basics Generic_AND-OR_Tree(s, successors, ?) [Generic_OR]](https://downloads.webis.de/lecturenotes/search/unit-en-basic-search3/unit-en-basic-search3-50.png)







![AND-OR Graph Search Basic_AND-OR_Tree(s, successors, is_solved) [Basic_OR]](https://downloads.webis.de/lecturenotes/search/unit-en-basic-search3/unit-en-basic-search3-58.png)





























![AND-OR Graph Search Generic_AND-OR(s, successors, ?) [Generic_AND-OR_Tree] [Generic_OR]](https://downloads.webis.de/lecturenotes/search/unit-en-basic-search3/unit-en-basic-search3-88.png)









![AND-OR Graph Search Basic_AND-OR(s, successors, is_solved) [Basic_OR]](https://downloads.webis.de/lecturenotes/search/unit-en-basic-search3/unit-en-basic-search3-98.png)


















































































































































![BF* Variants OPEN List Size Restriction: Best-First Beam Search [Rich & Knight 1991]](https://downloads.webis.de/lecturenotes/search/unit-en-informed-bf3/unit-en-informed-bf3-18.png)
















![Hybrid Strategies Strategy 4: Focal Search [Ibaraki 1978]](https://downloads.webis.de/lecturenotes/search/unit-en-informed-bf3/unit-en-informed-bf3-35.png)

![Hybrid Strategies Strategy 5: Staged Search [Nilson 1971]](https://downloads.webis.de/lecturenotes/search/unit-en-informed-bf3/unit-en-informed-bf3-37.png)

![Hybrid Strategies Strategy 6: Iterative Deepening A* – IDA* [Korf 1985]](https://downloads.webis.de/lecturenotes/search/unit-en-informed-bf3/unit-en-informed-bf3-39.png)






















































































![Evaluation of AND-OR Graphs ] Illustration of C ∗](https://downloads.webis.de/lecturenotes/search/unit-en-informed-bf5/unit-en-informed-bf5-35.png)



























![Systematic Search Categorization of Heuristic [Problem Solving] Methods](https://downloads.webis.de/lecturenotes/search/unit-en-representation1/unit-en-representation1-19.png)
![Systematic Search Categorization of Heuristic [Problem Solving] Methods](https://downloads.webis.de/lecturenotes/search/unit-en-representation1/unit-en-representation1-20.png)





















































![Problem-Reduction Representation Search Building Blocks [State-Space]](https://downloads.webis.de/lecturenotes/search/unit-en-representation2/unit-en-representation2-13.png)










































































































![Admissibility of A* Corollary 67 (Shallowest OPEN Node on Optimum Path [Lemma 62])?](https://downloads.webis.de/lecturenotes/search/unit-en-astar-formal1/unit-en-astar-formal1-62.png)
![Admissibility of A* Corollary 67 (Shallowest OPEN Node on Optimum Path [Lemma 62])?](https://downloads.webis.de/lecturenotes/search/unit-en-astar-formal1/unit-en-astar-formal1-63.png)




![Admissibility of A* Theorem 69 (Admissibility [Hart, Nilsson, Raphael 1968,1972])](https://downloads.webis.de/lecturenotes/search/unit-en-astar-formal1/unit-en-astar-formal1-68.png)
![Admissibility of A* Theorem 69 (Admissibility [Hart, Nilsson, Raphael 1968,1972])](https://downloads.webis.de/lecturenotes/search/unit-en-astar-formal1/unit-en-astar-formal1-69.png)










































































































































![Risk Measures Risk Measures of Type R(C) = %[C − f +]](https://downloads.webis.de/lecturenotes/search/unit-en-astar-relaxed2/unit-en-astar-relaxed2-24.png)
![Risk Measures Risk Measures of Type R(C) = %[C − f +]](https://downloads.webis.de/lecturenotes/search/unit-en-astar-relaxed2/unit-en-astar-relaxed2-25.png)




























































































| Shortcut | Documents |
|---|---|
|
↑/↓
|
Navigate documents |
|
Shift + ↑/↓
|
Navigate 3 documents |
| Shortcut | Pages |
|---|---|
|
←/→
|
Navigate pages |
|
Shift + MouseWheel
|
Navigate pages |
|
Shift + ←/→
|
Navigate 3 pages |